Wärmeverteilung im Filament

Welche Konstruktion ist für die Extruder-Düse optimal? Eine Recherche zeigt, dass einige der Meinung sind, dass die beheizte Strecke möglichst kurz sein soll, um "kleckern" zu verhindern. Das Problem ist dann aber die Wärme überhaupt in das Material zu bekommen. Hier habe ich mal die Wärmeübertragung von der Düse in das Filament unter folgenden Randbedingungen gerechnet:
1. Die Oberfläche vom Filament wird zum Zeitpunkt t=0 plötzlich von 20°C auf 240°C erhöht.
2. Wärmeleitung findet nur in radialer Richtung statt (wärmeübertragende Strecke ist groß im Vergleich zum Filament-Radius).
3. Die Stoffwerte von ABS sind: Dichte = 1,1 g/cm^3, spez. Wärmekapazität = 1,3 J/(gK), Wärmeleitfähigkeit = 0,18 W/(mK).
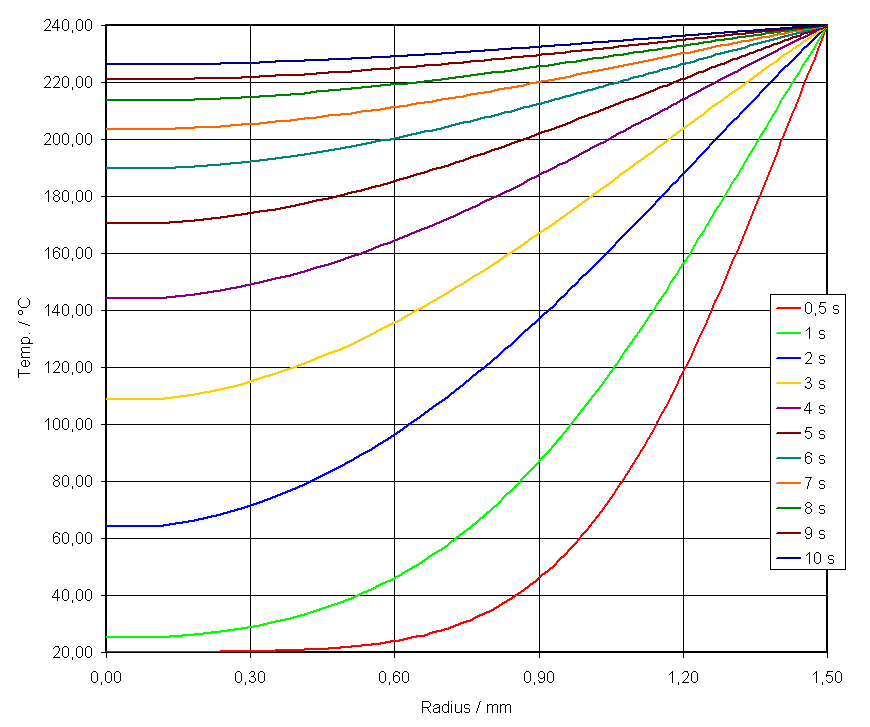
Das Ergebnis ist in folgender Grafik dargestellt:

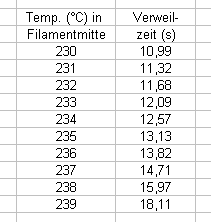
R = 1,5 mm ist die Filamentoberfläche, R=0 die Filamentmitte. Es ist zu sehen, dass das Material nicht "plötzlich" warm wird, sondern eine gewisse Zeit braucht. nach 10 s sind in der Filamentmitte beispielsweise erst 226°C erreicht. Da gerade im interessanten Bereich um 240°C die Grafik schlecht abzulesen wäre hier noch ein paar weitere Werte in tabellarischer Form:

Wenn beispielsweise die Temperatur in Filamentmitte nur 5°C unter der eingestellten Temperatur liegen soll, dann sind rund 13 s Verweilzeit in der Düse erforderlich. Wenn die Düse 15 mm lang ist, dann darf die Vorschubgeschwindigkeit max. 15/13 = 1,15 mm/s betragen, was die Druckgeschwindigkeit auf 1,15 * (3/0,5)^2 = 41,5 mm/s begrenzt.

Wenn hohe Druckgeschwindigkeiten bei "sauberer" Erwärmung des Materials erreicht werden sollen, dann müssen die Düsen lang sein.

Dem Einwand, dass in langen Düsen mehr flüssiges Material ist, welches bei einem retract herauskleckern kann, steht folgende Überlegung entgegen: Flüssigkeiten sind praktisch inkompressibel und dehnen sich bei einem retract nicht wesentlich aus. Deshalb kann die Menge flüssigen Kunststoffes nicht entscheidend sein. Zumindest dann, wenn der flüssige Kunststoff Solltemperatur erreicht hat. Material unterhalb der Solltemperatur wird bei einem Extruder-Stopp noch weiter erwärmt und kann durch die Wärmedehnung zum Kleckern führen. Insofern kommt es also nicht auf die flüssige, sondern auf die unvollständig erwärmte Materialmenge an, die gerade in kurzen Düsen sehr hoch ist.

Advance-Algorithmus

Mattroberts (Mattroberts' Firmware) schlägt auf Basis der Bernoulli-Gleichung vor, den Extruder beim Beschleunigen überproportional schnell laufen zu lassen, wobei die Anzahl der zusätzlichen Schritte gemäß n_extra = k v² berechnet wird. Dabei ist k eine Proportionalitätskonstante (advance Faktor) und v die eigentlich erforderliche Extruder-Geschwindigkeit.

Nach meiner Ansicht ist die quadratische Abhängigkeit nicht richtig, da sie sich nur bei turbulenten Strömungen ergibt. Siehe: Wikipedia-Bernoulli

Wenn die Strömung laminar ist, dann ist der Druckverlustbeiwert ζ nicht konstant, sondern selbst von der Geschwindigkeit abhängig (L_D = Rohrlänge, d = Rohrdurchmesser, Re = Reynoldszahl):

ζ = 64 L_D / (Re d) mit

Re = ρ v d / η = Dichte * Geschwindigkeit * Durchmesser / Viskosität

Quelle z.B.: Rohrreibungszahl

Damit ergibt sich für den Druckverlust in der Bernoulli-Gleichung: Δp = 32 η L_D v / d², was auch als Hagen-Poiseuille-Gesetz bezeichnet wird (hier ist jetzt Δp linear proportional zu v!).

Wenn jetzt mit konkreten Werten (η = 1000 Pa s, L_D = 2 mm, d = 0.5 mm, v = 60 mm/s) nur in der Düsenspitze gerechnet wird, dann ergibt sich Δp = 153.6 bar. Gegen diesen Wert sind alle anderen Druckverluste vernachlässigbar (dies zeigt auch, warum es so schwierig ist, mit kleinen Düsendurchmessern zu drucken). Auch die Querschnittsverengung spielt keine Rolle, da nur bei turbulenten Strömungen Wirbel auftreten, die zu einem nennenswerten Druckverlust führen.

Der Druckverlust führt zu einer elastischen Stauchung des Filaments zwischen Filamentschraube und Schmelzzone (Länge L_F, ca. 30 mm). Die Längenänderung ΔL_F kann gemäß

ΔL_F = L_D Δp / E

berechnet werden, wobei E das Elastizitätsmodul ist (bei ABS ungefähr 2000 MPa). Mit obigen Zahlenwerten ergibt sich ΔL_F = 0,23 mm. Dieses ΔL_F muß der Extruder während der Beschleunigungsphase zusätzlich vorschieben und beim Abbremsen entsprechend wieder einsparen.

Bei der folgenden Argumentation werden die klassischen Formelzeichen s für Weg, v für Geschwindigkeit, t für Zeit und k für eine Konstante benutzt. Bei konstanter Beschleunigung a ist v = a t und s = 0,5 a t². Am Ende der Beschleunigungsphase soll s aber um ΔL_F länger sein und während der Beschleunigung soll der zusätzliche Weg jederzeit proportional zu v sein (s.o.). Dies kann durch folgenden Ansatz erreicht werden:

v = a (t + k) und damit: s = a (0,5 t² + k t)

Der Term a k kann als eine "Zusatzgeschwindigkeit" interpretiert werden. Beim Abbremsen ist diese Zusatzgeschwindigkeit negativ anzusetzen. Grafisch sieht das Ganze so aus:

Ein Video mit "sehr langsamen" Einstellungen zeigt die Effekte auch recht deutlich: Advance-YouTube-Video

Interessant ist, dass beim Abbremsen ein "retract" ganz automatisch und zwangsläufig auftritt. Daher wurde bei den folgenden Tests der retract von 1 mm auf 0,3 mm reduziert. Bei Beschleunigungen zwischen 300 und 3000 mm/s² und Geschwindigkeiten von 13 - 107 mm/s lag k bei 40, wobei die in der Firmware verwendete Einheit noch unklar ist.

Druckparameter bei den Bildern: ABS, 230°C, v_max = 80 mm/s, v_Perimeter = 57 mm/s, a = 750 mm/s², jerk = 3, k = 40, oberes bzw. rechtes Teil ohne k.