Pendeluhr frei nach Harrison

Abb. 1: Sekundenpendeluhr mit einer Barometer-Kompensation nach Harrison

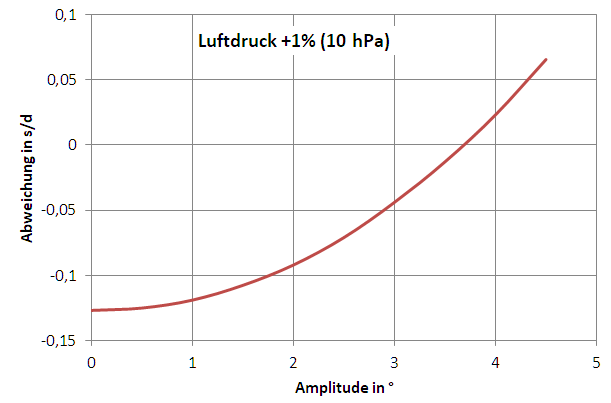
Abb. 2: Zusammenhang zwischen dem Gangfehler und der Pendelamplitude bei einer Luftdruckänderung

Harrisons Vermächtnis

Im Jahr 1775 hat John Harrison, der bereits das Längengrad-Problem bei der Navigation auf See mittels einer sehr genauen Uhr gelöst hatte, seine Überlegungen zu einer optimalen Pendeluhr in einem Manuskript zusammengefasst (siehe 'Concerning Such Mechanism', eine "Übersetzung" von David Heskin). Anders als sein Zeitgenosse Graham, dessen Hemmung noch heute häufig in Präzisionspendeluhren eingesetzt wird, wollte Harrison keine kleine Pendel-Amplitude (um 1°) sondern eine sehr große um 7°. Ihm war dabei durchaus bewusst, dass die Schwingungsdauer mit zunehmender Amplitude ebenfalls minimal zunimmt (die exakte Lösung für die Schwingungsdauer ist in "Mathematisches Pendel" zu finden). Wenn die Schwingungsdauer zunimmt, dann wird die Uhr langsamer, d.h. sie geht nach.

Andererseits kann eine Pendeluhr durch äußere Einflüsse auch vorgehen. Das ist der Fall, wenn die Luftdichte sinkt (bei sinkendem Druck oder bei steigender Temperatur), da dann die Luftreibung (c_w-Wert) sinkt und das Pendel weniger abbremst. Weiterhin verringert sich der Luftauftrieb, was dazu führt, dass das Pendelgewicht steigt. Dabei steigt nur das Gewicht (Rückstellkraft bei der Schwingung), aber nicht die Masse (Trägheit des Pendels gegen die Rückstellkraft). Die träge Masse wird sogar geringer, da die mitbewegte Luft leichter wird. Das alles kann sehr einfach in der Gleichung für die Periodendauer T eines Pendels mit der Länge L berücksichtigt werden (g = Erdbeschleunigung, ρ_L = Luftdichte, ρ_P = Pendeldichte):

T = 2 π [(ρ_P + f ρ_L) L / {(ρ_P - ρ_L) g}]^1/2

Der Faktor f für die vom Pendel mitbewegte Luft liegt zwischen ca. 0,5 beim Linsenpendel und etwa 1 beim Zylinderpendel. Die Herleitung der Gleichung ist in "T-Luftdichte.pdf" kurz skizziert. Wird mit dieser Gleichung (mit f = 1) der Gangfehler einer Sekundenpendeluhr bei 1 hPa Luftdruckabnahme berechnet, dann ergeben sich +0,013 s/d (Sekunden pro Tag). Dieser Wert stimmt gut mit Literaturangaben überein. Neben dem schnelleren Gang der Uhr steigt auch die Pendel-Amplitude leicht an, da die erhöhte Rückstellkraft dem Pendel mehr Energie zuführt und die Luftreibung abnimmt.

Harrisons Erkenntnis war nun, dass der Gangfehler durch Luftdichteänderungen bei einer ausreichend großen Amplitude ganz automatisch durch die Abhängigkeit der Schwingungsdauer von der Amplitude ausgeglichen wird. Genial! Allerdings waren Harrisons Zeitgenossen misstrauisch und erst im Jahr 2015 wurde nachgewiesen, dass Harrisons Ansatz funktioniert: "Video: Amazingly accurate clock...". Diese Uhr wird im folgenden - wie auch im Video - "Clock B" genannt.

Berechnungen zu Harrisons Kompensation

Praktisch unmittelbar nachdem ich in der Tageszeitung von der Clock B gelesen und noch einen Artikel von Betts (pdf: Harrison's Barometric Compensation) gefunden hatte, war ich von dem Konzept überzeugt und habe erste Berechnungen angestellt. Ausgangspunkt dabei war einerseits obige Gleichung und andererseits die Reibungsarbeit W_R die das Pendel bei der Bewegung durch die Luft verrichten muss (gerechnet wurde mit einem Edelstahl-Kugelpendel mit dem Durchmesser D = 70 mm):

W_R = F_R s_P ( = Reibungskraft mal Pendelweg), wobei

F_R = 0,5 ρ_L v_P² c_w π D²/4   ist.

Darin sind der Pendelweg s_P und die mittlere Pendelgeschwindigkeit v_P:

s_P = 2 L φ   und   v_P = 2 s_P / T   (mit der Amplitude φ im Bogenmaß).

Der Widerstandsbeiwert c_w wurde nach Kaskas (3. Seite) berechnet. Mit diesen Gleichungen wird jetzt zuerst die Reibungsarbeit bei "normalem" Druck (z.B. 1000 hPa) für eine vorgegebene Pendelamplitude berechnet. Dann wird der Druck geändert (z.B. um 1% erhöht) und die Pendelamplitude wird durch Ausprobieren solange verändert, bis die neu berechnete Reibungsarbeit mit der ursprünglichen übereinstimmt. Mit den beiden Pendelamplituden kann jetzt die oben zitierte exakte Lösung der Schwingungsdauer "gefüttert" und in Sekunden pro Tag umgerechnet werden.

Diese Berechnungen wurden für vorgegebene Amplituden zwischen 0 und 4,5° mehrfach ausgeführt und in Abb. 2 zusammengefasst. Bei 0° Amplitude geht die Uhr entsprechend der ersten Gleichung um 0,127 s/d nach, wenn der Druck um 10 hPa erhöht wird. Dieser Nachgang wird mit steigender Amplitude immer geringer, bis bei 3,7° eine vollständige Druckkompensation erreicht ist. Prinzipiell entspricht dies der Vorhersage von Harrison doch er sprach von 7° und die Clock B kompensiert den Druck bei etwas über 6°. Wie ist das zu erklären?

Harrison hatte an der Pendelfeder-Einspannung zirkulare Backen vorgesehen (explizit keine Huygensschen Backen, mit denen die Kompensation nicht funktionieren würde) und solche zirkularen Backen sind in der Clock B auch verbaut. Die Backen führen dazu, dass sich mit zunehmender Amplitude die Pendellänge verkürzt und die Schwingungsdauer zunächst sogar mit der Amplitude abnimmt, bevor sie bei sehr großen Amplituden wieder steigt. Betts (s.o.) bezeichnet die konstruktive Abstimmung von Backen und Pendelfeder als "hill tests". Erst nach dem Berg ergeben sich abnehmende s/d-Werte mit zunehmender Amplitude.

Wenn die Einspannung der Pendelfeder - wie heutzutage üblich - scharfkantig erfolgt, dann gibt es keinen Berg bzw. der höchste Punkt des Berges liegt bei 0° Amplitude. Dadurch tritt die Druck-Kompensation bei deutlich kleineren Amplituden auf. Das ist auch gut so, da bei einer Amplitude unter 4° wohnzimmertaugliche Uhren mit der Harrison-Kompensation gebaut werden können :-)

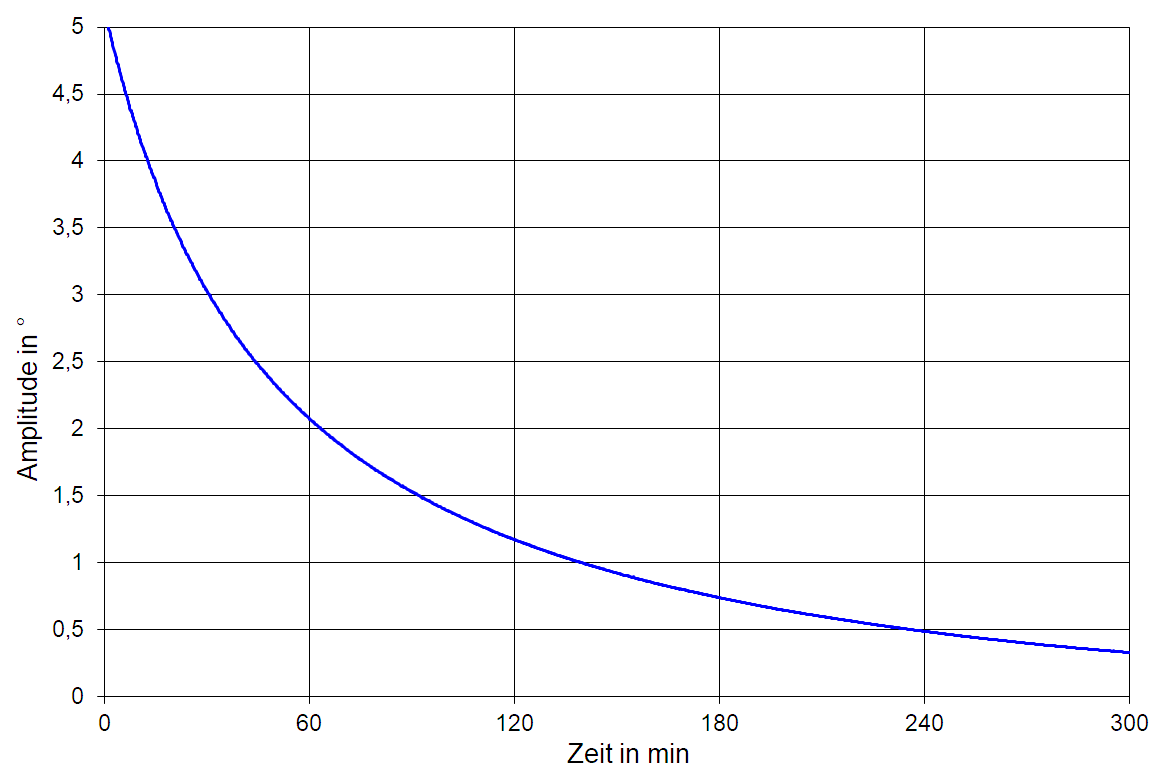
Abb. 3: Abklingversuch zur Bestimmung des Energiebedarfs bei großen Amplituden

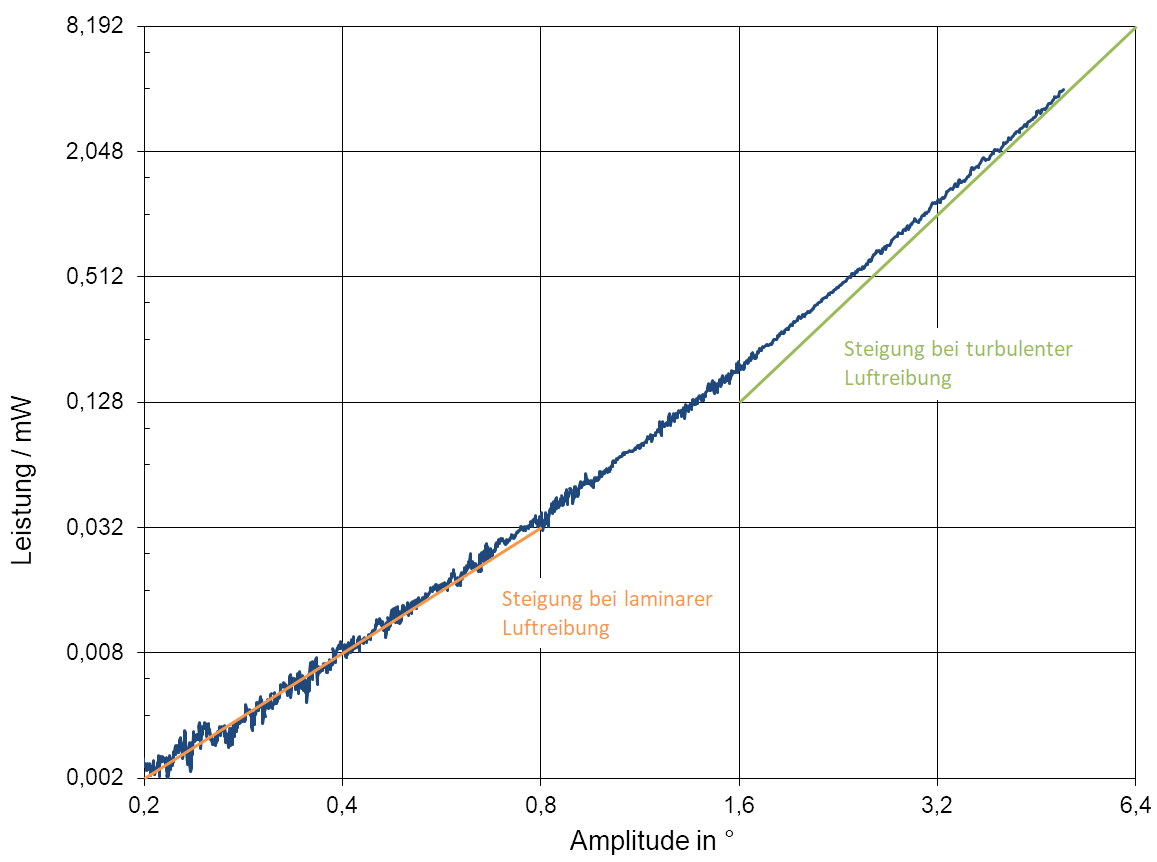
Abb. 4: Auswertung des Abklingversuchs: Pendelleistung

Überlegungen zur Auslegung der Uhr

Ein Pendel, dass mit 4° Amplitude schwingt hat 16-mal mehr Energie gespeichert, als es bei 1° hätte. Während jeder Halbschwingung (1 s) gibt es im wesentlichen durch Luftreibung einen kleinen Teil der Energie ab, der durch die Hemmung ersetzt werden muss. Wenn die Luftreibung laminar ist, dann ist die Reibungskraft proportional zur Geschwindigkeit und der Energieverlust (Kraft mal Weg) proportional zu Geschwindigkeit und Amplitude. Bei dem 4° zu 1° Verhältnis wäre der Energiebedarf der Uhr also um den Faktor 16 höher. Bei turbulenter Luftreibung beträgt der Faktor sogar 64, da die Reibungskraft dann proportional zum Quadrat der Geschwindigkeit ist.

Um den Faktor etwas genauer zu bestimmen, wurde folgender Abklingversuch durchgeführt (siehe auch Abb. 3): Das Pendel (damals noch ein Kugelpendel mit 80 mm Durchmesser und einem Gewicht von m = 2 kg) wurde um gut 5° ausgelenkt und dann losgelassen wodurch es frei (ohne Antrieb / Hemmung) schwingen konnte. Dabei verliert es Energie und die Amplitude wird immer kleiner. Die Zeit und die zugehörige Schwingungsamplitude wurden mittels Zeitwaage aufgezeichnet. Nach gut 5 h wurde der Versuch beendet. Aus 2 Amplitudenwerten φ₁ und φ₂ im zeitlichen Abstand Δt kann jetzt der Energieverlust ΔE berechnet werden:

ΔE = E₂ - E₁   mit   E_i = m g L (1 - cos(φ_i)), i = 1, 2

Wird der Energieverlust noch durch den Zeitunterschied Δt geteilt, dann ergibt sich die erforderliche Leistung P:

P = ΔE / Δt   mit der Einheit W bzw. mW

In Abb. 4 ist die so berechnete Leistung dargestellt. Es ist zu sehen, dass "normale" Sekundenpendeluhren mit ca. 1° Amplitude fast im Bereich der laminaren Luftreibung liegen (Die beiden Kurvensteigungen für laminare und turbulente Reibung sind in dem Diagramm als Geraden zur besseren Qrientierung mit eingetragen). Bei der größten gemessenen Amplitude von 5° wird die Steigung für turbulente Reibung nahezu erreicht. Eine Auswertung der dem Diagramm zugrunde liegenden Zahlenwerte ergibt für 4° Amplitude eine 37-fache Leistung im Vergleich zu 1°. Es ist also fast nicht möglich, die Uhr als Monatsläufer auszulegen. Gewählt wurde ein Tagesläufer.

Abb. 5: Schwerkrafthemmung mit Kniehebelchen

Der letzte Abschnitt hat gezeigt, dass die Steigerung von 1° auf 4° Amplitude einerseits die Pendelenergie E um den Faktor 16 erhöht, dass aber andererseits die 37-fache Energie ΔE pro Periode zugeführt werden muss. Im Sinne des Qualitätsfaktors Q = E / ΔE, der üblicherweise zur Beurteilung von Pendeln verwendet wird, tritt also eine Verschlechterung ein. Dies hat auch Van Baak (siehe auch Pendulum Accuracy) für die Clock B festgestellt und sich gefragt, wieso die Uhr trotzdem so genau geht. Er kommt zu dem Ergebnis, dass die Hemmung frei von Störungen (z.B. Räderwerkseinfluss) sein muss und definiert neben Q noch einen "purity factor".

Um den Räderwerkseinfluss zu minimieren fiel die Wahl auf eine Schwerkrafthemmung. Festgelegt wurde auch im Vorfeld, dass die Hebung über ca. 3° erfolgen soll (1° vor und 2° nach der Nulllage des Pendels). Das entspricht etwa den Verhältnissen bei einer Graham-Hemmung, die bei bei einer Auslegung für 1° Amplitude typischerweise ebenfalls 1° Hebung hat (1/3° vor der Nulllage und 2/3° danach). Um 3° Hebung mit einer Graham-Hemmung zu erreichen, müssten die Paletten extrem schräg angestellt werden, was hohe Reibungsverluste und evtl. sogar eine Blockade mit sich brächte. Daher erfolgte die Konstruktion mit den Kniehebeln, die in Abb. 5 zu sehen sind.

Schwerkrafthemmungen haben den Ruf "durchzurattern" wie mir im Uhrenwerkstattforum mitgeteilt wurde und leider trat das Problem auch mit dieser Hemmung auf. Abhilfe schafft eine Wirbelstrombremse die aus einer 1,5 mm dünnen Aluscheibe auf der Ankerradwelle und 8 Neodymmagneten besteht. Die Magnete sind in eine Plexiglasscheibe eingelassen und diese ist mit der vorderen Platine verschraubt. Leider sind die Magnete nicht so schön und deshalb wurde der eigentlich größer geplante Einblick in das Räderwerk verkleinert.

Abb. 7: Pendelfeder. Die Klemmung des Quarzglasstabes erfolgt genau auf Höhe der Auflage.

Abb. 8: die Pendellinse ist aus 8 Edelstahlscheiben mit jeweils 6 mm Dicke zusammengesetzt.

Aufbau des Getriebes zur Mondphase mit 105247 / 3564 ≈ 29,5306 Tagen Lunationsdauer. Der Fehler ist also kleiner als 0,5 s, während die übliche Untersetzung mit 29,5 Tagen einen Fehler von 44 min aufweist.

Schraubgewichte zur Anpassung der Amplitude

Aufzugsmotor

Zeitwaage in der Schublade

Die Zeitwaage sendet die Daten auch per WLAN ins Heimnetz

Das Ziffernblatt

Wirbelstrombremse im Räderwerk

Räderwerk von links gesehen

Gegengewichtskette zur Antriebskette

China-Motor (defekt) und neuer Faulhaber-Motor

Update 24.04.2022:

Nach knapp 4 Jahren hat der Aufzugsmotor aufgegeben. Bei der Demontage fanden sich feinste und auch gröbere Partikel im Uhrgehäuse, die aller Wahrscheinlichkeit nach von den Kohlebürsten des Motors stammen (Abrieb). Dies und die enttäuschende Lebensdauer führten zu dem Entschluss einen Brushless-Motor einzusetzen, wobei die Auswahl an kurz bauenden Getriebemotoren sehr überschaubar ist. Zum Einsatz kommt jetzt ein Faulhaber-Motor mit 22 mm Durchmesser der an der Abtriebswelle praktisch die gleiche Leistung liefert, wie der China-Motor mit 33 mm Durchmesser. Für die Ohren ist der neue Motor ein Wohltat, für den Geldbeutel nur dann, wenn sich der 20-fache Preis auch entsprechend in der Lebensdauer bemerkbar macht. Aktuell hängt der Motor an einem China-Controller, da Faulhaber die benötigten Chips für den eigentlich eingeplanten Controller nicht bekommt und der Liefertermin in den Sternen steht.